![[picoCTF 2022] Sequences](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2Fc2Wuv6%2FbtrA53OwyAG%2FkeJ3PSmkDXk5yv5NZo20Vk%2Fimg.png)
1. Investigation
Hint#1 : Google "matrix diagonalization". Can you figure out how to apply it to this function?
문제 설명을 살펴보니 자신이 만들어 놓은 “선형 재귀 함수”를 빠르게 동작하도록 만들어 Flag 를 획득하라고 합니다.
힌트#1 에서는 "matrix diagonalization" 을 구글링해서 어떻게 함수에 적용할 수 있을지 생각해보라고 하네요.
2. Solution
주어진 파일부터 확인해보겠습니다.
import math
import hashlib
import sys
from tqdm import tqdm
import functools
ITERS = int(2e7)
VERIF_KEY = "96cc5f3b460732b442814fd33cf8537c"
ENCRYPTED_FLAG = bytes.fromhex("42cbbce1487b443de1acf4834baed794f4bbd0dfb5df5e6f2ad8a2c32b")
# This will overflow the stack, it will need to be significantly optimized in order to get the answer :)
@functools.cache
def m_func(i):
if i == 0: return 1
if i == 1: return 2
if i == 2: return 3
if i == 3: return 4
return 55692*m_func(i-4) - 9549*m_func(i-3) + 301*m_func(i-2) + 21*m_func(i-1)
# Decrypt the flag
def decrypt_flag(sol):
sol = sol % (10**10000)
sol = str(sol)
sol_md5 = hashlib.md5(sol.encode()).hexdigest()
if sol_md5 != VERIF_KEY:
print("Incorrect solution")
sys.exit(1)
key = hashlib.sha256(sol.encode()).digest()
flag = bytearray([char ^ key[i] for i, char in enumerate(ENCRYPTED_FLAG)]).decode()
print(flag)
if __name__ == "__main__":
sol = m_func(ITERS)
decrypt_flag(sol)소스코드를 살펴보니 이미 복호화 함수가 구현되어 있어서 그냥 돌려보면 Flag 가 나올 듯 해보였습니다.
RecursionError: maximum recursion depth exceeded
하지만 당연하게도 Flag 가 나오지 않았습니다.
에러 내용을 기반으로 검색해보니 재귀 함수에서 반복할 수 있는 최대 깊이를 넘어서면 해당 에러가 발생하는 것 같았습니다.
왜 이 에러가 발생하는지 소스코드를 다시 한번 면밀히 살펴보았습니다.
ITERS = int(2e7)
...
def m_func(i):
...
return 55692*m_func(i-4) - 9549*m_func(i-3) + 301*m_func(i-2) + 21*m_func(i-1)
...
if __name__ == "__main__":
sol = m_func(ITERS)
decrypt_flag(sol)main 에서 m_func 함수에 ITERS 를 인자로 주어 재귀적으로 반복하게 되는데 ITERS = int(2e7) 이라는 값이 20,000,000 (2천만) 이라서 최대 깊이를 넘어서기 때문에 발생하는 에러였습니다.
그렇다면 최대 깊이를 조정하면 될까요? 한번 해봤습니다.
if __name__ == "__main__":
sys.setrecursionlimit(ITERS)
print(sys.getrecursionlimit())
sol = m_func(ITERS)
decrypt_flag(sol)
당연하게도 되지 않았습니다. (더 큰 값을 줘도 마찬가지)
조정된 깊이를 출력하고 m_func 함수가 작동되는 듯 했으나 그냥 IDLE 쉘이 재시작되며 프로그램을 종료했습니다.
이제 어떻게 해야 할까요? 힌트#1 를 살펴보니 “Matrix diagonalization” 에 대해 구글링 해보라고 합니다.
https://en.wikipedia.org/wiki/Diagonalizable_matrix
(...?????????????)
(진짜 어지러웠습니다...🤢)
먼저 개념을 이해하기 위해서 한글로 된 정보들을 찾아보기 시작했습니다. (행렬 대각화)
https://soohee410.github.io/diagonalization
(내가 한글을 보고 있는게 맞나?)
전혀 이해가 안갔는데 한 문장이 눈에 들어왔습니다.
대각행렬로 표현하면 연산 과정이 간단해지고 해석이 용이하다는 등 장점이 많아지기 때문입니다!
음... 뭔가 대각행렬을 이용하면 연산 과정을 간단하게 만들 수 있나 봅니다. 일단 넘어가겠습니다.
이번 포스팅에서 다룰 내용은 바로 행렬의 대각화(Diagonalization)이다. 행렬의 대각화는 지난 시간에 배운 고유값(eigenvalue)과 고유벡터(eigenvector)를 활용하기 위한 하나의 방법이라고 할 수 있으며, 다른 말로는 고유값분해(Eigendecomposition) 라고도 불린다. 또한 행렬의 대각화를 통해 LU 분해, QR분해와 같이 행렬을 고유값과 고유벡터로 구성된 부분 행렬들로 분해할 수 있으며, 이는 어떤 반복적인 선형방정식을 풀 때 굉장히 유용한 특성을 가지고 있다. 대각화에 대해 공부해보자.
다른 블로그를 살펴보니 어떤 반복적인 선형방정식을 풀 때 행렬의 대각화를 굉장히 유용하게 사용할 수 있다고 합니다.
그런데 아직까지도 어떻게 풀어야할지 감이 안잡힙니다.
문제에서 자신이 “Linear recurrence function” 을 썼다고 했으니 비슷한 유형의 문제가 기존에 출제된 적이 있지 않을까 싶어서 “linear recurrence ctf” 와 같은 방식으로 키워드를 조합해 구글링해보았습니다.
(Matrix 를 선언하는 부분을 유심히 볼 것.)
https://scryptos.org/write-ups/pwn2win_ctf-2016/pwn2win_ctf-2016-writeup.html#death-sequence-ppc-100
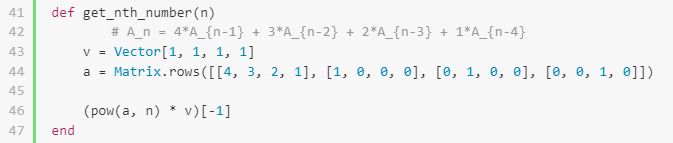
https://github.com/raccoons-team/ctf/tree/master/2016-03-28-pwn2win/death_sequence_100
Pwn2Win CTF 에서 출제된 Death Sequence 라는 문제에 대한 두 개의 Writeup 을 확인할 수 있었는데 각각 풀이는 달랐지만 어떠한 연속적인 Sequence 값을 이용해 함수 f(x) 를 정의하고 f(x) 의 계수를 취해 대각화 가능한 행렬 A 를 만들어 어떠한 정수 n 에 대한 f(n) 의 계산을 빠른 시간 내에 수행하는 것을 확인할 수 있었습니다.
이에 대한 예시로 가장 대표적인게 피보나치 수열입니다.
http://matrix.skku.ac.kr/2012-Sage/sage-la/4-2.htm
피보나치 수열에 대한 재귀식(점화식)은 f(x + 2) = f(x + 1) + f(x), 초기값은 f(0) = 0, f(1) = 1 과 같은데, f(x+1)의 계수(1), f(x)의 계수(1)를 취해 대각화 가능한 2x2 행렬 A 를 만들면 다음과 같습니다:
(1행은 계수 [1, 1] 이 들어가고 2행은 대각화 가능한 2x2 정방행렬을 만들기 위해 임의로 [1, 0] 을 넣어서 만듭니다)
(예를 들어, 2x2 가 아닌 4x4 정방행렬을 만드는 경우는 계수가 총 4개여야 하고
1행은 [계수 4개]가,
2행은 [1, 0, 0, 0],
3행은 [0, 1, 0, 0],
4행은 [0, 0, 1, 0]
과 같은 규칙으로 행렬이 만들어집니다.)
이제 피보나치 수열에 대한 행렬 A 를 대각화하여 A = P * D * PI 을 만족하는 행렬 P, 그에 대한 역행렬 PI, 그리고 행렬 D 를 모두 구할 수 있고, (컴퓨터가 계산해 줄 것임)
대각화 성질에 의해 A 의 k 승을 P * D^k * PI 을 이용해 빠르게 풀 수 있게 됩니다.
Proof)
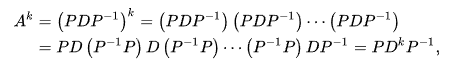
근데 왜 갑자기 A 의 k 승을 구할까요?
만약 우리가 피보나치 수열의 10000 번째에 있는 수가 무엇인지 구하고 싶을 때 A 의 10000 승을 빠르게 계산할 수 있는 P * D^10000 * PI 에 초기벡터(f(1) = 1, f(0) = 0)를 곱해주면 (f(10000 + 1), f(10000)) 와 같은 식으로 10001 번째 수와 10000 번째 수를 쉽게 알아낼 수 있기 때문입니다. (!!!)
(위 링크의 예시에서는 피보나치 수열의 11 번째 수와 10 번째 수를 알아냈음)
(아래는 그 예시)
(x0 은 초기벡터. x0 = (1, 0))
(0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...)
결론
응용
위와 같은 개념을 숙지한 상태로 본격적인 문제 풀이에 들어가겠습니다.
문제에서 제공하는 소스코드의 m_func 부분을 보면 아래와 같습니다:
def m_func(i):
if i == 0: return 1
if i == 1: return 2
if i == 2: return 3
if i == 3: return 4
return 55692*m_func(i-4) - 9549*m_func(i-3) + 301*m_func(i-2) + 21*m_func(i-1)이를 재귀식으로 표현해보면 return 부분을 보았을 때 f(x) = 55692 * f(x - 4) - 9549 * f(x - 3) + 301 * f(x - 2) + 21 * f(x - 1) 이 되며, 초기값은 f(0) = 1, f(1) = 2, f(2) = 3, f(3) = 4 입니다.
f(x) 의 작은 계수부터 취하여 행렬 A 를 만듭니다.
초기벡터 x0 = (f(3) = 4, f(2) = 3, f(1) = 2, f(0) = 1) 을 만듭니다.
위에서 따로 설명하지는 않았지만, 행렬 D 를 만들기 위해 행렬 A 의 고유값(eigenvalue)을 구합니다.
(컴퓨터가 알아서 계산)
고유값을 이용해 행렬 D 를 만듭니다. 아래와 같이 대각선 방향으로 고유값을 넣어주면 됩니다.
행렬 A 의 고유벡터(eigenvector)를 구합니다.
(컴퓨터가 알아서 계산)
고유벡터를 이용해 행렬 P 를 만듭니다. 고유벡터의 행과 열을 바꿔서 만들어주면 됩니다.
행렬 P 의 역행렬 PI 를 구합니다.
(컴퓨터가 알아서 계산)
A = P * D * PI 를 만족하는지 확인합니다.
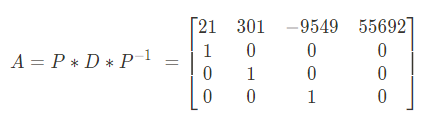
(컴퓨터가 알아서 계산)
올바른 행렬 P, D, PI 를 구했음을 확인할 수 있습니다.
이제 k = 20000000 일 때, P * (D ^ k) * PI * x0 를 계산하여 solution = (f(k + 3), f(k + 2), f(k + 1), f(k)) 를 구하면 f(k) 에 대한 값을 알 수 있게 됩니다.
최종적으로 구한 f(k) 을 decrypt_flag 함수의 인자로 넣어 복호화를 진행하면 Flag 를 획득할 수 있습니다.
>> Sequences-sol.sage
# REF#1 - Diagonalization (대각화) : <http://matrix.skku.ac.kr/2012-Sage/sage-la/4-1.htm>
# REF#2 - Recurrence Relations (재귀 관계): <http://matrix.skku.ac.kr/2012-Sage/sage-la/4-2.htm>
# REF#3 - Application to matrix functions (행렬 대각화 응용): <https://en.wikipedia.org/wiki/Diagonalizable_matrix>
# REF#4 - CTF writeup : <https://scryptos.org/write-ups/pwn2win_ctf-2016/pwn2win_ctf-2016-writeup.html#death-sequence-ppc-100>
# REF#5 - CTF writeup : <https://github.com/raccoons-team/ctf/tree/master/2016-03-28-pwn2win/death_sequence_100>
# REF#6 - 행렬 대각화를 이용한 n차 정방행렬의 p제곱 구하기 : <https://rfriend.tistory.com/183>
'''
# Source code of sequences.py
ITERS = int(2e7)
...
def m_func(i):
if i == 0: return 1
if i == 1: return 2
if i == 2: return 3
if i == 3: return 4
return 55692*m_func(i-4) - 9549*m_func(i-3) + 301*m_func(i-2) + 21*m_func(i-1)
def decrypt_flag(sol):
...
if __name__ == "__main__":
sol = m_func(ITERS)
decrypt_flag(sol)
문제 요약 : 위 재귀함수를 컴퓨터가 계산이 가능하도록 최적화 하여
ITERS 값을 넣었을 때의 결과값을 복호화한 뒤 FLAG 를 얻어라.
제공 힌트 : "Matrix Diagonalization" (행렬 대각화) 에 대해 구글링 해보시오.
'''
# Implemented in SageMath
# f(x) => m_func(x)
# f(x) = 55692 * f(x - 4) - 9549 * f(x - 3) + 301 * f(x - 2) + 21 * f(x - 1)
# f(0) = 1, f(1) = 2, f(2) = 3, f(3) = 4
# Take coefficients from f(x) to make 4 by 4 matrix A.
A = matrix([[21, 301, -9549, 55692], [1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0]])
print("[+] Matrix A: ")
print(A)
print()
# 초기벡터 선언
# Vector x0 equals to (f(3), f(2), f(1), f(0)) = (4, 3, 2, 1).
print("[+] Vector x0: ")
x0 = vector([4, 3, 2, 1])
print(x0)
print()
# 대각 행렬 D를 만들기 위한 행렬 A의 고유값 구하기
print("[+] Eigenvalues: ")
print(A.eigenvalues()) # [17, 13, 12, -21]
print()
# Generate digonal matrix D with eigenvalues.
print("[+] Digonal Matrix D: ")
D = matrix([[17, 0, 0, 0], [0, 13, 0, 0], [0, 0, 12, 0], [0, 0, 0, -21]])
print(D)
print()
# 행렬 A를 대각화하는 행렬 P를 만들기 위한 행렬 A의 고유벡터 구하기
print("[+] Taking columns of Eigenvetors: ")
ev = A.eigenvectors_right()
print(ev[0][1][0]) # (1, 1/17, 1/289, 1/4913)
print(ev[1][1][0]) # (1, 1/13, 1/169, 1/2197)
print(ev[2][1][0]) # (1, 1/12, 1/144, 1/1728)
print(ev[3][1][0]) # (1, -1/21, 1/441, -1/9261)
print()
# 행렬 P
# transpose() 메소드를 이용해 행과 열 교환
print("[+] Matrix P: ")
P = matrix([ev[0][1][0], ev[1][1][0], ev[2][1][0], ev[3][1][0]]).transpose()
print(P)
print()
# 검증
print("[+] Check A = PDP^(-1): ")
PI = P.inverse()
print(A == P*D*PI)
print()
assert A == P*D*PI
import hashlib
VERIF_KEY = "96cc5f3b460732b442814fd33cf8537c"
ENCRYPTED_FLAG = bytes.fromhex("42cbbce1487b443de1acf4834baed794f4bbd0dfb5df5e6f2ad8a2c32b")
def decrypt_flag(sol):
sol = sol % (10**10000)
sol = str(sol)
sol_md5 = hashlib.md5(sol.encode()).hexdigest()
# sol_md5 must be same as VERIF_KEY.
print("[+] MD5(sol): ", sol_md5)
if sol_md5 != VERIF_KEY:
print("Incorrect solution")
return
key = hashlib.sha256(sol.encode()).digest()
flag = bytearray([char ^^ key[i] for i, char in enumerate(ENCRYPTED_FLAG)]).decode()
# XOR operation in SageMath is ^^, not ^.
print(flag)
# Same as ITERS in sequences.py
k = int(2e7) # 20,000,000
# 행렬의 대각화를 이용해 행렬의 n 승을 효율적으로 구할 수 있다.
# A ^ n = (P * D * P ^ (-1)) ^ n = P * D ^ n * P ^ (-1)
# 왜 갑자기 행렬의 n 승을 구하는가?
# 행렬의 n 승에 초기벡터 x0 를 곱해주면 (x_n+3, x_n+2, x_n+1, x_n) 과 같이
# f(n + 3), f(n + 2), f(n + 1), f(n) 에 대한 값을 구할 수 있기 때문에
# f(k) = f(20000000) 를 효율적으로 구할 수 있게 된다.
# sol = (x_n+3, x_n+2, x_n+1, x_n)
sol = P * (D ^ k) * PI * x0
# sol[3] = x_k
decrypt_flag(sol[3])
# picoCTF{b1g_*******_a1c77d6c}
# Output
'''
[+] Matrix A:
[ 21 301 -9549 55692]
[ 1 0 0 0]
[ 0 1 0 0]
[ 0 0 1 0]
[+] Vector x0:
(4, 3, 2, 1)
[+] Eigenvalues:
[17, 13, 12, -21]
[+] Digonal Matrix D:
[ 17 0 0 0]
[ 0 13 0 0]
[ 0 0 12 0]
[ 0 0 0 -21]
[+] Taking columns of Eigenvetors:
(1, 1/17, 1/289, 1/4913)
(1, 1/13, 1/169, 1/2197)
(1, 1/12, 1/144, 1/1728)
(1, -1/21, 1/441, -1/9261)
[+] Matrix P:
[ 1 1 1 1]
[ 1/17 1/13 1/12 -1/21]
[ 1/289 1/169 1/144 1/441]
[ 1/4913 1/2197 1/1728 -1/9261]
[+] Check A = PDP^(-1):
True
[+] MD5(sol): 96cc5f3b460732b442814fd33cf8537c
picoCTF{b1g_*******_a1c77d6c}
'''
🚩 FLAG : picoCTF{b1g_*******_a1c77d6c}
'CTF writeups > Crypto' 카테고리의 다른 글
| [Cyber Apocalypse CTF 2022] The Three-Eyed Oracle (0) | 2022.05.20 |
|---|---|
| [Cyber Apocalypse CTF 2022] Jenny From The Block (0) | 2022.05.20 |
| [picoCTF 2022] NSA Backdoor (0) | 2022.05.04 |
| [picoCTF 2022] Sum-O-Primes (0) | 2022.05.04 |
| [picoCTF 2022] Very Smooth (0) | 2022.05.03 |